轻松学会：如何表示平角

揭秘平角的神秘面纱：全面解析平角的表示方法与奇妙应用

在几何学的广阔天地里，平角如同一道独特的风景线，既普通又神秘。它不仅是度量角的基本单位之一，还蕴含着丰富的数学知识和应用价值。那么，平角究竟是什么？它又是如何表示出来的呢？让我们一起揭开平角的神秘面纱，探寻它的奥秘。

一、平角的定义与基本特征

平角，顾名思义，是一个与平面相关的角。在数学上，平角被定义为角度等于180°的角。换句话说，当你把一个圆分成两个相等的部分时，每一部分所对应的圆心角就是一个平角。平角的基本特征在于它的度数是固定的，不随图形的缩放而改变，这为我们在几何计算和证明中提供了极大的便利。

二、平角的多种表示方法

平角的表示方法多种多样，每种方法都有其独特的优点和适用场景。接下来，我们将详细介绍几种常见的平角表示方法。

1. 弧度制表示法

在数学中，除了角度制外，还有一种更为简洁的表示角的方法——弧度制。在弧度制下，平角对应的数值是π（圆周率）。这种表示方法尤其在三角函数和微积分等领域中具有广泛应用。使用弧度制表示平角，不仅使得公式的推导更加简洁，而且能够揭示出许多与圆相关的几何性质。

2. 图形表示法

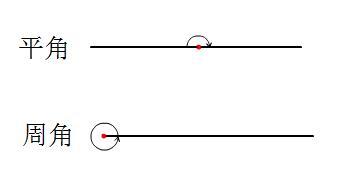
图形表示法是直观展示平角的有效手段。一个最简单的图形表示法是绘制一条直线，然后将这条直线看作是一个由两个反向排列的直角组成的平角。此外，还可以通过绘制一个半圆并标注出圆心角的方式来表示平角。这种图形化的表示方法使得平角的概念更加易于理解和记忆。

3. 符号表示法

在几何学著作和数学文献中，平角通常用特定的符号来表示。例如，在数学公式中，平角可以写作“180°”或“π（弧度）”。而在一些特定的几何图形中，则可能采用更抽象的符号来表示平角，如使用一个带有箭头或点的线段来表示角的方向和大小。这些符号的引入，使得几何问题的描述更加准确和严谨。

4. 度量衡表示法

在现实生活中，平角的概念还可以通过度量衡来表示。例如，在建筑施工中，当两条墙壁成180°夹角时，我们称之为“平角墙”。这种表示方法使得平角的概念与实际生活紧密相连，增加了学习的趣味性和实用性。

三、平角的奇妙应用

平角不仅在几何学领域中占据着重要地位，还在物理学、工程学以及日常生活等多个领域中发挥着重要作用。以下是平角在一些领域中的奇妙应用实例。

1. 物理学中的平角

在物理学中，平角的概念被广泛应用于光的反射和折射规律中。当光线从一个介质射向另一个介质时，反射光线、入射光线和法线三者之间的夹角关系与平角密切相关。此外，在波动理论中，波的叠加和干涉现象也与平角有关。这些应用使得平角成为物理学中一个不可或缺的概念。

2. 工程学中的平角

在工程学中，平角的概念在结构设计和材料力学中具有重要意义。例如，在桥梁设计中，为了确保桥梁的稳定性和承载能力，需要精确计算桥墩之间的夹角以及桥梁与地面的夹角。这些夹角往往接近于平角或包含平角的部分。同样地，在机械设计中，齿轮的啮合角度、传动轴的夹角等都与平角有关。这些应用展示了平角在工程学中的实用价值。

3. 日常生活中的平角

在日常生活中，平角的概念同样无处不在。例如，当我们站在一个角落时，这个角落所形成的夹角就是一个平角。此外，在看电视时，屏幕上的画面也呈现出一个平角的形状。这些日常生活中的实例使得平角的概念更加贴近我们的生活和实际体验。

四、探索平角的更深层次奥秘

平角作为一个基础而重要的几何概念，其背后还隐藏着许多更深层次的奥秘。随着数学和物理学的发展，人们对平角的认识也在不断深化和拓展。

1. 平角与三角函数的关系

三角函数是数学中一个重要的工具，它涉及到角度与边长之间的数量关系。在平角的情况下，三角函数具有一些特殊的性质。例如，正弦函数在平角处取值为0，余弦函数在平角处取值为-1，而正切函数在平角处则趋于无穷大。这些性质为我们在处理包含平角的几何问题时提供了有用的线索和依据。

2. 平角在复平面上的应用

复平面是数学中一个重要的概念，它将实数与复数联系起来，形成一个完整的数系。在复平面上，平角对应于单位圆上从正实轴到负实轴的旋转。这种旋转操作不仅在数学上具有重要意义，而且在信号处理、图像处理等领域中也有广泛应用。

3. 平角与非欧几何的关系