标准误的计算方法是什么？

在统计学中，标准误是一个至关重要的概念，它用于衡量样本统计量（如均值、比例等）的估计值与总体真实值之间的误差大小。对于希望深入了解统计分析方法的研究者来说，掌握标准误的计算公式及其背后的原理显得尤为重要。本文旨在详细阐述标准误的定义、计算公式及其在统计分析中的应用，以期帮助读者更好地理解和运用这一概念。

标准误，顾名思义，是衡量样本统计量估计误差的标准量。在统计学中，我们通常通过样本数据来推断总体特征，而样本统计量（如样本均值）与总体真实值之间总会存在一定的误差。这种误差的大小不仅取决于样本容量，还与总体的分布特征有关。标准误正是用于量化这种误差大小的指标，它反映了样本统计量估计的精确度。

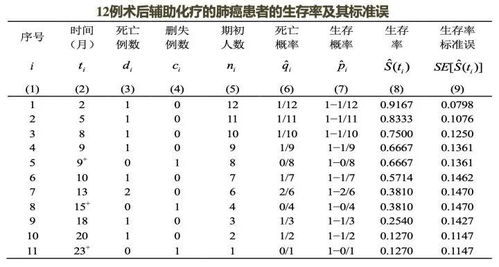
标准误的计算公式主要取决于所研究的样本统计量类型。对于最常见的样本均值来说，标准误的计算公式为：标准误 = 标准差 / 样本容量的平方根。其中，标准差是衡量数据离散程度的统计量，它反映了数据点与均值之间的平均差异；而样本容量则是指样本中包含的观测值数量。这个公式表明，随着样本容量的增加，标准误会逐渐减小，即样本均值的估计会越来越精确。

为了更直观地理解标准误的计算过程，我们可以通过一个具体的例子来说明。假设我们有一个包含100个观测值的样本，这些观测值来自一个正态分布的总体，其标准差为σ。我们计算得到样本均值为X̄，现在我们希望估计这个样本均值与总体真实均值μ之间的误差大小。根据标准误的计算公式，我们可以将样本标准差s（作为总体标准差σ的估计值）除以样本容量的平方根√n，得到标准误SE(X̄)。这个标准误值就是我们对样本均值估计误差的量化指标。

值得注意的是，标准误的计算不仅适用于样本均值，还适用于其他类型的样本统计量，如样本比例、样本方差等。对于不同类型的样本统计量，标准误的计算公式会有所不同。例如，对于样本比例来说，其标准误的计算公式通常涉及样本比例本身、样本容量以及总体比例（如果已知）等因素。因此，在实际应用中，我们需要根据所研究的样本统计量类型选择相应的标准误计算公式。

标准误在统计分析中具有广泛的应用价值。首先，它是构建置信区间的基础。置信区间是一种用于估计总体参数的统计方法，它给出了一个包含总体真实参数值的区间范围，并给出了这个区间包含真实值的概率（即置信水平）。标准误的大小直接决定了置信区间的宽度：标准误越小，置信区间越窄，即我们对总体参数的估计越精确。

其次，标准误还用于计算假设检验的统计量。在假设检验中，我们通常需要根据样本数据来检验某个关于总体的假设是否成立。标准误作为衡量样本统计量估计误差的指标，可以帮助我们计算检验统计量的值，并据此判断假设是否成立。例如，在t检验中，我们需要计算样本均值与假设的总体均值之间的差异与标准误的比值（即t值），然后根据t分布表来判断这个差异是否显著。

此外，标准误还常用于样本量的确定。在进行统计分析之前，我们通常需要确定一个合适的样本量以确保结果的可靠性。标准误作为衡量样本统计量估计精确度的指标，可以帮助我们评估不同样本量下估计结果的稳定性。一般来说，样本量越大，标准误越小，估计结果越稳定可靠。因此，在确定样本量时，我们需要权衡考虑研究成本、时间等因素与标准误之间的关系。

然而，在实际应用中，我们还需要注意一些可能影响标准误计算准确性的因素。例如，样本的选择方式（如随机抽样、分层抽样等）会对标准误产生影响；样本数据的异常值或缺失值也可能导致标准误的计算结果出现偏差。因此，在进行统计分析之前，我们需要对样本数据进行仔细的检查和预处理以确保结果的准确性。

总之，标准误是衡量样本统计量估计误差的重要指标，在统计分析中具有广泛的应用价值。通过掌握标准误的计算公式及其背后的原理，我们可以更好地理解和运用统计分析方法来解决实际问题。同时，我们还需要注意在实际应用中可能影响标准误计算准确性的因素，并采取相应的措施来确保结果的可靠性。