数学中ln 1 的值是多少
在数学领域中,自然对数(通常以符号“ln”表示)是一个非常重要的概念,它源自约翰·纳皮尔斯在17世纪对于对数的研究,并由莱昂哈德·欧拉在18世纪正式命名和推广。自然对数是以数学常数e(约等于2.71828)为底的对数,其独特的性质在微积分、物理学、工程学、经济学等多个领域都有广泛的应用。当我们谈论“ln 1等于多少”时,实际上是在探索自然对数函数在特定值(即1)上的行为。
数学背景与自然对数的定义
要理解“ln 1等于多少”,首先需要明确自然对数的定义。对数函数可以被看作是指数函数的逆运算。具体来说,如果a^x = N(a > 0,且a ≠ 1),那么x就叫做以a为底N的对数,记作x = log_a N。当a = e时,我们得到的就是自然对数,记作x = ln N。这里,e是一个无理数,也是自然对数的底数,它在数学和物理中有着举足轻重的地位。

ln 1的计算过程
现在,我们来探讨“ln 1等于多少”的问题。根据自然对数的定义,如果ln x = y,则意味着e^y = x。为了找到ln 1的值,我们需要找到一个y,使得e^y = 1。
在数学上,任何数的0次方都等于1(除了0的0次方在数学中是未定义的),因此e^0 = 1。由此我们可以推断出,当x = 1时,y = 0,即ln 1 = 0。
自然对数函数的性质
为了更好地理解ln 1 = 0这一结果,我们可以进一步探讨自然对数函数的一些基本性质:
1. 定义域与值域:自然对数函数的定义域是所有正实数(即(0, +∞)),值域是所有实数(即R)。这意味着,对于任何正实数N,都存在一个实数y,使得e^y = N;反之亦然。
2. 单调性:自然对数函数在其定义域上是严格单调递增的。这意味着,如果x1 < x2,则ln x1 < ln x2。这一性质使得自然对数函数在解决不等式问题时非常有用。
3. 极限性质:当x趋近于0时,ln x趋近于负无穷;当x趋近于正无穷时,ln x趋近于正无穷。这反映了自然对数函数在极值情况下的行为。
4. 对数的运算法则:自然对数函数遵循对数的运算法则,如ln(ab) = ln a + ln b(当a > 0且b > 0时),ln(a/b) = ln a - ln b(当a > 0且b > 0且b ≠ 0时),以及ln(a^n) = n ln a(当a > 0且n为实数时)。这些运算法则大大简化了涉及自然对数的计算过程。
ln 1的实际意义与应用
虽然ln 1 = 0这一结果看似简单,但它在数学和实际应用中却有着深远的意义。以下是一些具体的例子:
1. 微积分中的应用:在微积分中,自然对数函数经常出现在积分和微分问题中。了解ln 1 = 0这一事实有助于我们解决与自然对数相关的微积分问题。例如,在计算涉及e^x或ln x的函数的定积分时,我们可能需要利用这一性质来简化计算过程。
2. 经济学中的应用:在经济学中,复利计算和连续复利计算都涉及到自然对数。了解ln 1 = 0有助于我们理解这些计算背后的数学原理。例如,在计算连续复利下的本金增长倍数时,我们可能会用到自然对数函数。
3. 物理学中的应用:在物理学中,自然对数函数经常出现在描述衰变、增长和扩散等过程的方程中。了解ln 1 = 0有助于我们理解这些方程的物理意义并求解相关问题。
4. 数据分析与机器学习:在数据分析和机器学习领域,自然对数函数也扮演着重要角色。例如,在处理具有极端值的数据集时,我们可能会使用自然对数函数来进行数据变换,以改善模型的性能。了解ln 1 = 0有助于我们正确地应用这些变换方法。
结论
综上所述,“ln 1等于多少”这一问题的答案是0。这一结果不仅反映了自然对数函数在特定值上的行为,还揭示了自然对数函数的一些基本性质和实际应用。通过深入理解这些概念和性质,我们可以更好地应用自然对数函数来解决实际问题,并在数学、物理学、经济学等多个领域取得更深入的见解和进展。
自然对数作为数学中的一个基本概念,
- 上一篇: 怎样制作QQ上的闪图照片秀?
- 下一篇: PS安装抽出滤镜插件的简易教程
-
 探索非零条件下a、b、c的奇妙组合:揭秘a+a+b+b+c+c的值资讯攻略12-05
探索非零条件下a、b、c的奇妙组合:揭秘a+a+b+b+c+c的值资讯攻略12-05 -
 鬼谷八荒游戏角色最高魅力值是多少资讯攻略01-22
鬼谷八荒游戏角色最高魅力值是多少资讯攻略01-22 -
 200000000等于多少万资讯攻略11-07
200000000等于多少万资讯攻略11-07 -
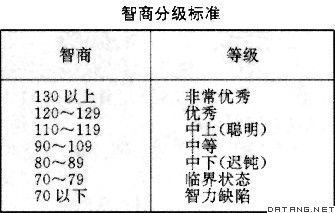 IQ正常值范围及等级划分标准资讯攻略12-06
IQ正常值范围及等级划分标准资讯攻略12-06 -
 棋盘上交叉点总数是多少,为何?资讯攻略11-25
棋盘上交叉点总数是多少,为何?资讯攻略11-25 -
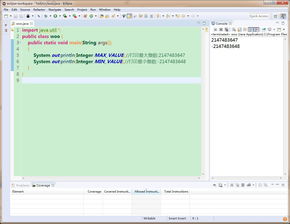 如何计算变量int dt的值?资讯攻略12-02
如何计算变量int dt的值?资讯攻略12-02












