小学四年级奥数题:如何加一条直线将图形划分为两个三角形?
小学四年级奥数题详解:加一条直线,把图形划分成两个三角形

这是一道经典的奥数题,适合小学四年级的学生挑战。题目要求我们在一个给定的图形中加一条直线,使得这个图形被划分成两个三角形。这听起来可能有些复杂,但通过一步步的分析和推理,我们会发现,其实这个问题并没有那么难。
首先,我们来观察图形。题目中并没有给出具体的图形,但为了讲解方便,我们可以假设一个常见的图形,比如一个平行四边形或者一个不规则的四边形。不过,由于这是一道奥数题,我们不需要局限于特定的图形,而是要掌握一种通用的方法。
方法分析:
1. 观察图形特点:
我们需要仔细观察图形的边和角,看看是否存在一些特殊的性质,比如是否有直角、等腰、等边等特点。这些特点可能会给我们提供划分图形的线索。
2. 尝试添加直线:
在脑海中或者在纸上尝试添加不同的直线,看看哪些直线可以将图形划分成两个三角形。不要急于得出结论,要多尝试几种可能性。
3. 利用几何知识:
我们可以利用三角形的内角和为180度、平行线的性质等几何知识来帮助我们确定直线的位置。
现在,我们来具体演示一下如何在不同的图形中添加一条直线,将其划分成两个三角形。
示例一:平行四边形
假设我们有一个平行四边形ABCD,其中AB平行于CD,AD平行于BC。我们的目标是通过添加一条直线,将这个平行四边形划分成两个三角形。
1. 观察特点:
平行四边形有两组对边平行,且对角相等。
2. 尝试添加直线:
我们可以尝试从平行四边形的一个顶点出发,画一条到对边(但不是相邻边)的直线。比如,从顶点A出发,画一条直线到边CD上的一点E(E不是C或D)。
3. 验证结果:
这样,我们就得到了两个三角形ABE和CDE。其中,ABE由顶点A、B和E组成,CDE由顶点C、D和E组成。通过验证,我们可以发现这两个三角形都满足三角形的性质,即有三个角和三条边。
示例二:不规则四边形
现在,我们来处理一个更复杂的情况,即一个不规则四边形ABCD,其中没有任何一组对边平行,也没有任何一组对角相等。
1. 观察特点:
不规则四边形没有特殊的性质,我们需要通过尝试和推理来找到划分的方法。
2. 尝试添加直线:
由于不规则四边形没有明显的对称性或平行性,我们需要更加灵活地尝试添加直线。一个可能的方法是,选择四边形的一个顶点,比如A,然后尝试从A出发画一条到四边形内部某一点E(E不在四边形的任何一条边上)的直线。这条直线需要满足的条件是,它能够将四边形划分成两个三角形。
3. 调整直线位置:
通过移动点E的位置,我们可以调整直线的方向。我们需要找到一个合适的位置,使得直线AE能够将四边形ABCD划分成两个三角形。这可能需要一些试错和调整,但只要我们保持耐心和细心,就一定能找到正确的位置。
4. 验证结果:
一旦我们找到了合适的位置和直线,就可以通过验证来确认我们的答案是正确的。比如,我们可以检查两个三角形是否都有三个角和三条边,以及它们的内角和是否都为180度。
通用方法:
通过上面的示例,我们可以总结出一种通用的方法来解决这个问题:
1. 选择起点:
首先,选择四边形的一个顶点作为起点。
2. 确定终点:
然后,在四边形的内部或另一个边上选择一个点作为终点。这个点可以是任意的,但我们需要确保从起点到终点的直线能够将四边形划分成两个三角形。
3. 画出直线:
使用直尺或铅笔,从起点到终点画出一条直线。
4. 验证结果:
最后,检查两个三角形是否都满足三角形的性质。如果不满足,我们需要重新选择终点并画出新的直线。
需要注意的是,虽然这个问题看似简单,但实际上它考察了我们对几何图形的理解和分析能力。通过不断地尝试和调整,我们可以培养出更加灵活和创造性的思维方式。
此外,这个问题还有一个更广泛的应用场景。在现实生活中,我们经常会遇到需要将一个复杂的事物或问题分解成几个简单部分的情况。这时,我们就可以借鉴这个问题的解决方法,通过找到一个合适的“切入点”或“划分线”,将整体分解成几个易于处理的部分。这样不仅可以降低问题的难度,还可以提高我们的工作效率和解决问题的能力。
综上所述,通过添加一条直线将图形划分成两个三角形是一个既有趣又富有挑战性的奥数问题。它不仅考察了我们对几何图形的理解和分析能力,还培养了我们的创造性和解决问题的能力。希望这篇文章能够帮助你更好地理解这个问题,并在未来的学习和生活中应用到类似的方法。
- 上一篇: 揭秘!简溪致林萧的情书究竟藏在哪一章?
- 下一篇: 如何查询中国石油卡积分
-
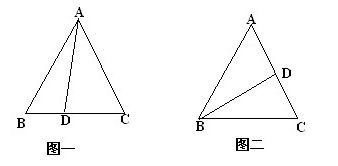 直线分割成两个三角形的图解资讯攻略11-27
直线分割成两个三角形的图解资讯攻略11-27 -
 一年级小学数学精品教学合集,打造孩子的数学乐园!资讯攻略11-21
一年级小学数学精品教学合集,打造孩子的数学乐园!资讯攻略11-21 -
 六年级数学宝典:爱上数学学习合集资讯攻略11-14
六年级数学宝典:爱上数学学习合集资讯攻略11-14 -
 小学数学园地中《二年级数学》教学合集有哪些内容?资讯攻略10-31
小学数学园地中《二年级数学》教学合集有哪些内容?资讯攻略10-31 -
 打造小学六年级精彩记忆:创意时间轴绘制指南资讯攻略11-18
打造小学六年级精彩记忆:创意时间轴绘制指南资讯攻略11-18 -
 如何教学《小学英语精通版三年级下册》的技巧合集?资讯攻略11-07
如何教学《小学英语精通版三年级下册》的技巧合集?资讯攻略11-07












