圆周率的尽头:人类能否揭开其无限之谜?
圆周率,这个数学世界中既古老又神秘的无理数,自古以来就吸引着无数数学家和爱好者的目光。它不仅是圆的周长与直径之比,更是连接几何与代数、有限与无限、确定与随机的奇妙桥梁。在历史的长河中,人类对圆周率的探索从未停歇,而对于“圆周率可能被算尽吗”这一问题,更是引发了无数猜想与讨论。

首先,我们需要明确的是,圆周率π是一个无理数。这意味着它不能表示为两个整数的比,其小数部分是无限不循环的。这一性质早在古希腊时期就被数学家们所发现,并成为了数学研究中的一个重要课题。随着数学理论的不断发展,尤其是微积分和级数理论的诞生,数学家们开始尝试用更加精确的方法来计算圆周率。从阿基米德的几何方法,到刘徽的“割圆术”,再到祖冲之和祖暅的密率,每一次进步都极大地推动了数学的发展。

然而,尽管我们已经能够计算出圆周率的数以亿计的小数位数,但关于它是否可能被算尽的问题,却始终没有明确的答案。这一问题的核心在于无理数的本质。无理数的小数部分是无限不循环的,这意味着我们无法通过一个有限的过程来完全确定它的所有小数位。因此,从这个角度来看,圆周率似乎是不可能被算尽的。

然而,数学界并不乏对圆周率可能被算尽的猜想。这些猜想往往源于对数学基础的深刻思考和新的数学理论的提出。例如,有数学家提出,如果数学的基础公理体系发生改变,那么圆周率是否可能被算尽的问题也可能随之改变。这种猜想虽然具有挑战性,但也为数学研究提供了新的思路和方向。

此外,还有一些数学家试图从物理学的角度来探讨圆周率是否可能被算尽的问题。他们认为,圆周率作为一个物理常数,其值可能与宇宙的微观结构和宏观性质有关。如果宇宙的微观结构或宏观性质发生某种未知的变化,那么圆周率的值也可能随之改变。当然,这种猜想目前还缺乏确凿的证据来支持,但它却为我们提供了一种全新的思考角度。
除了数学和物理学的角度外,还有一些哲学家和数学家从逻辑和证明的角度来探讨这个问题。他们认为,圆周率是否可能被算尽的问题实际上是一个关于数学真理的问题。在数学中,真理通常是通过证明来确定的。然而,对于圆周率这样的无理数来说,我们无法通过一个有限的过程来证明其所有小数位的值。因此,从这个角度来看,圆周率似乎也是不可能被算尽的。
然而,值得注意的是,数学的发展往往伴随着新的数学理论和工具的诞生。随着计算机科学的飞速发展,我们已经能够利用高速计算机和先进的算法来计算圆周率的更多小数位数。这种计算能力的提升不仅让我们对圆周率有了更加深入的了解,也为数学研究提供了新的方法和工具。因此,未来是否会有新的数学理论或工具出现,使得我们能够完全确定圆周率的所有小数位,仍然是一个值得期待的问题。
当然,对于圆周率是否可能被算尽的问题,也有人持乐观态度。他们认为,随着人类对数学和物理学的不断探索和深入,我们终将有一天能够揭开圆周率的神秘面纱。这种乐观态度虽然鼓舞人心,但也需要我们保持理性和谨慎。毕竟,数学作为人类智慧的结晶,其深度和广度远远超出了我们的想象。在这个充满未知和挑战的领域里,我们需要保持敬畏之心,不断探索和前进。
此外,关于圆周率的研究并不仅仅局限于其是否可能被算尽的问题。事实上,圆周率在数学、物理学、工程学等多个领域都有着广泛的应用。例如,在物理学中,圆周率与波动现象、量子力学等都有着密切的联系;在工程学中,圆周率则是计算圆的周长、面积等几何量的基础。因此,对于圆周率的研究不仅具有理论意义,也具有重要的实用价值。
综上所述,圆周率是否可能被算尽的问题是一个复杂而深刻的问题。它涉及到数学、物理学、逻辑学等多个学科领域的知识和理论。尽管我们已经能够计算出圆周率的数以亿计的小数位数,但关于其是否可能被完全确定的问题仍然是一个未解之谜。然而,这并不影响我们对圆周率的热爱和探索。相反,正是这种未知和挑战激发了人类不断前进的动力和智慧。在未来的日子里,让我们继续携手前行,在数学的海洋中探索更多的未知和奇迹吧!
- 上一篇: 如何在支付宝查询2021年成绩?
- 下一篇: 如何将健康码绑定到另一个手机号码
-
 怎样在圆周率π中找到自己的生日日期?资讯攻略11-14
怎样在圆周率π中找到自己的生日日期?资讯攻略11-14 -
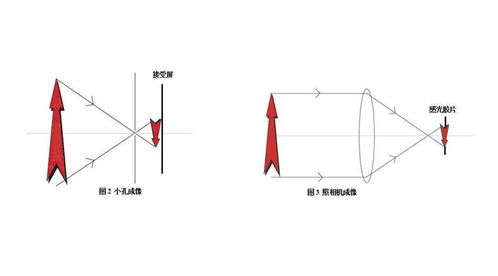 小孔成像原理能否用来观测日食?资讯攻略11-22
小孔成像原理能否用来观测日食?资讯攻略11-22 -
 E63手机乐园签名解锁:能否畅享塞班论坛专属软件?资讯攻略12-05
E63手机乐园签名解锁:能否畅享塞班论坛专属软件?资讯攻略12-05 -
 唐朝女子梳妆铜镜清晰度:能否清晰映照人像?蚂蚁庄园解析资讯攻略11-22
唐朝女子梳妆铜镜清晰度:能否清晰映照人像?蚂蚁庄园解析资讯攻略11-22 -
 探寻明日之后:揭秘彩虹天堂的异常之处资讯攻略11-16
探寻明日之后:揭秘彩虹天堂的异常之处资讯攻略11-16 -
 吸血鬼骑士:第三季剧情深度解析与预告资讯攻略10-24
吸血鬼骑士:第三季剧情深度解析与预告资讯攻略10-24











