Excel中计算几何平均数的方法
在数据处理与分析的广阔领域中,Excel作为一款功能强大的电子表格软件,广泛应用于各行各业,从基础的财务数据统计到复杂的数学模型构建,无所不包。其中,求解几何平均数作为数据分析的一个重要环节,对于理解数据集的整体趋势和特性具有重要意义。几何平均数,与算术平均数不同,它更侧重于反映数据序列中各数值之间的乘积关系,特别适用于处理增长率或比例类数据。以下,我们就来详细探讨在Excel中如何高效准确地求出几何平均数。
一、几何平均数的概念与重要性
几何平均数(Geometric Mean, GM)是指n个正实数乘积的n次方根,常用于处理具有指数增长或衰减特性的数据集。相比算术平均数,几何平均数能更好地反映数据的“平均增长率”或“平均倍数”,因为它会考虑到数据中所有数值的相对大小和它们之间的乘积效应。例如,在财务分析中,使用几何平均数来衡量复利投资回报率时,能更准确地反映出长期投资的平均表现。
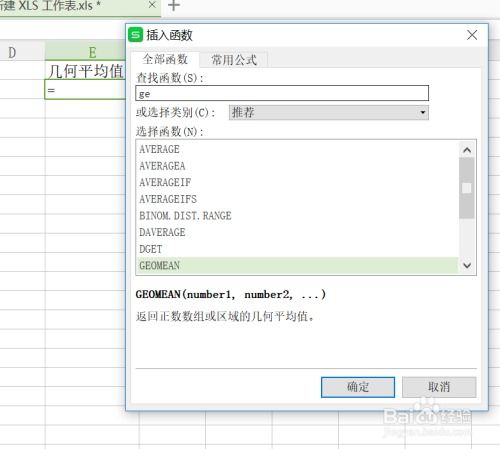
二、Excel中求解几何平均数的方法
在Excel中,虽然没有直接的几何平均数函数(如SUM用于求和,AVERAGE用于求算术平均),但我们可以通过一些数学公式和Excel的内置函数组合来实现几何平均数的计算。以下介绍几种常见的方法:
方法一:使用POWER和PRODUCT函数组合
对于一组数据,我们可以利用`PRODUCT`函数计算所有数值的乘积,然后用`POWER`函数求该乘积的n次方根(n为数据个数),从而得到几何平均数。这种方法适用于数据项较少且易于直接操作的情况。
假设在Excel的A1:A5单元格区域中有一组数据,计算其几何平均数的公式为:
```excel
=POWER(PRODUCT(A1:A5), 1/COUNT(A1:A5))
```
这里,`PRODUCT(A1:A5)`计算A1到A5区域内所有数值的乘积,`COUNT(A1:A5)`计算该区域内数值的个数(不包括空白或错误值),然后通过`POWER`函数将该乘积的n次方根计算出来,即得到几何平均数。
方法二:使用数组公式
对于更复杂的数据处理或需要频繁计算几何平均数的情况,可以考虑使用Excel的数组公式。虽然现代版本的Excel已经支持动态数组(无需手动按Ctrl+Shift+Enter),但了解传统数组公式的使用仍然有助于应对一些特殊情况。
一个简化的数组公式示例(在现代Excel中无需按Ctrl+Shift+Enter)如下:
```excel
=(PRODUCT(A1:A5))^(1/COUNTA(A1:A5))
```
注意,这里使用了`COUNTA`而不是`COUNT`,因为`COUNTA`会计算区域内非空单元格的数量,包括数值、文本和逻辑值,这在某些特定情况下可能更加适用。不过,在计算几何平均数时,通常我们只关心数值型数据,因此`COUNT`更为常见。
方法三:使用辅助列和AVERAGE函数(间接法)
如果数据集较为复杂,或者你想以更直观的方式理解计算过程,可以通过在辅助列中使用对数转换,然后计算转换后数据的算术平均数,最后通过反对数转换回原数据尺度的方法间接求得几何平均数。
1. 在辅助列(比如B列)中,对每个数值取自然对数,公式为`=LN(A1)`(假设数据在A列)。
2. 使用`AVERAGE`函数计算B列中所有对数值的算术平均数。
3. 将得到的算术平均数进行反对数转换,即使用`EXP`函数,公式为`=EXP(AVERAGE(B1:B5))`,从而得到原数据集的几何平均数。
这种方法虽然步骤较多,但通过对数转换,可以更清晰地看到几何平均数与算术平均数之间的关系,以及它们如何分别反映数据的不同特性。
三、总结
在Excel中求解几何平均数,虽然没有直接的函数支持,但通过合理利用Excel提供的`PRODUCT`、`POWER`、`COUNT`(或`COUNTA`)、`AVERAGE`、`LN`、`EXP`等函数,我们可以灵活地计算出所需的几何平均数。选择哪种方法,取决于具体的数据集特点、个人偏好以及分析需求。无论采用哪种方式,掌握几何平均数的计算方法,都将有助于你更深入地理解数据,做出更加精准的决策。
-
 Excel快速计算指定店铺商品销售总额的方法资讯攻略12-09
Excel快速计算指定店铺商品销售总额的方法资讯攻略12-09 -
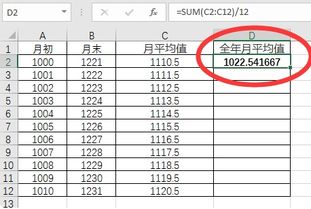 如何轻松计算资产总额(全年平均数)?资讯攻略11-26
如何轻松计算资产总额(全年平均数)?资讯攻略11-26 -
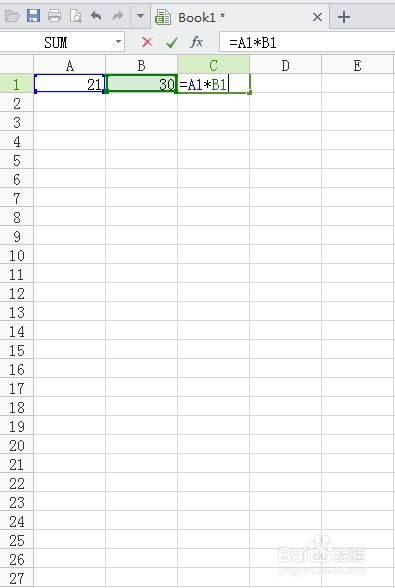 Excel表格轻松掌握求积技巧资讯攻略11-09
Excel表格轻松掌握求积技巧资讯攻略11-09 -
 Q&A: 快速掌握!Excel小技巧——如何轻松对含分类小计的表格求总计?资讯攻略11-22
Q&A: 快速掌握!Excel小技巧——如何轻松对含分类小计的表格求总计?资讯攻略11-22 -
 Excel达人秘籍:轻松掌握在表格中输入乘号的绝妙技巧!资讯攻略10-25
Excel达人秘籍:轻松掌握在表格中输入乘号的绝妙技巧!资讯攻略10-25 -
 Excel技巧:一键速算债券贴现率,轻松掌握财务分析工具资讯攻略10-25
Excel技巧:一键速算债券贴现率,轻松掌握财务分析工具资讯攻略10-25












