空心方阵的计算公式是什么
空心方阵的公式解析

空心方阵问题在数学和实际应用中经常出现,其公式和计算方法对于解决这类问题至关重要。本文将详细介绍空心方阵的定义、公式推导以及应用,帮助读者深入理解并掌握这一知识点。
一、空心方阵的定义
空心方阵,顾名思义,是一种中间为空心的方形阵列。具体来说,它是由若干层正方形组成,但最中心部分没有元素填充。常见的空心方阵有奇数层和偶数层之分,但无论是奇数层还是偶数层,其计算方式都有一定的规律可循。
二、空心方阵的公式推导
1. 奇数层空心方阵
对于奇数层的空心方阵,我们可以从最外层开始,逐层向内计算。假设最外层每边有n个元素,那么:
最外层元素总数为4n - 4(因为四个角各有一个元素被重复计算了)。
次外层每边比最外层少2个元素,所以元素总数为4(n-2) - 4。
依次类推,直到最内层。
对于奇数层方阵,假设层数为k(k为奇数),则总元素个数S可以表示为:
S = 4n - 4 + 4(n-2) - 4 + ... + 4[n-(k-1)*2] - 4
= 4[n + (n-2) + ... + (n-(k-1)*2)] - 4k/2
= 4[n*k/2 - (0 + 2 + ... + (k-1)*2)/2] - 2k
= 2nk - 2k² + 2k
其中,n表示最外层每边的元素个数,k表示层数。
2. 偶数层空心方阵
对于偶数层的空心方阵,情况稍微复杂一些。假设最外层每边有n个元素,那么:
最外层元素总数依然为4n - 4。
但从第二层开始,每层的每边元素个数不再是简单地减2,而是根据层数的奇偶性有所不同。具体来说,当层数为偶数时,每层的每边元素个数比上一层少2;当层数为奇数时(在偶数层方阵中,从外往内数第二层算作奇数层),每层的每边元素个数与上一层相同或减4(取决于上一层的每边元素个数是否为偶数)。
不过,为了简化计算,我们可以将偶数层方阵看作是由两个奇数层方阵(一个稍大,一个稍小)相减得到的“空心部分”。即,我们可以先计算出一个比实际偶数层方阵稍大的奇数层方阵的总元素个数,再减去一个比实际偶数层方阵稍小的奇数层方阵的总元素个数。
假设偶数层方阵的最外层每边有n个元素,层数为2k(k为正整数),则总元素个数S可以表示为:
S = (2nk - 2k² + 2k) - [(2(n-k)-2)k - 2k² + 2k]
= 2nk - 2k² + 2k - (2nk - 4k² - 2kn + 2k² - 2k + 2k)
= 4k(n-k)
其中,n表示最外层每边的元素个数,2k表示层数。
三、空心方阵公式的应用
1. 计算总元素个数
根据上面推导出的公式,我们可以直接计算出空心方阵的总元素个数。无论是奇数层还是偶数层方阵,都只需要知道最外层每边的元素个数和层数即可。
2. 解决实际问题
空心方阵公式在解决实际问题中有广泛应用。例如,在军事上布置防御工事时,需要计算士兵的站位数量;在体育活动如方阵表演中,需要计算参与者的数量;在建筑设计如花坛布置中,需要计算花卉的数量等。这些问题都可以通过空心方阵公式得到快速准确的解答。
3. 拓展应用
除了直接计算总元素个数外,空心方阵公式还可以用于解决一些更复杂的问题。例如,当方阵中的元素不是简单的计数对象而是具有某种特定属性(如重量、面积等)时,我们可以通过计算总元素个数来间接求出这些属性的总和。此外,当方阵的形状或大小发生变化时(如由正方形变为长方形或梯形等),我们也可以在空心方阵公式的基础上进行适当的变形和扩展来解决新问题。
四、注意事项
在使用空心方阵公式时,需要注意以下几点:
1. 准确理解题意:要仔细阅读题目并准确理解其要求,确保所给条件(如最外层每边的元素个数、层数等)正确无误。
2. 正确选择公式:要根据方阵的层数(奇数层还是偶数层)选择正确的公式进行计算。
3. 注意公式的适用范围:空心方阵公式适用于计算由正方形元素组成的空心方阵的总元素个数,对于其他形状或不规则排列的元素则不适用。
4. 计算结果要合理验证:在计算完成后,要对结果进行合理性验证,确保其符合实际情况和题目要求。
五、总结
空心方阵公式是一种用于计算由正方形元素组成的空心方阵总元素个数的数学工具。通过本文的介绍和分析,我们了解了空心方阵的定义、公式推导以及应用方法。在实际应用中,我们可以根据题目的要求和条件选择合适的公式进行计算,并注意公式的适用范围和注意事项。希望本文能够帮助读者更好地理解和掌握空心方阵公式这一知识点。
- 上一篇: 揭秘:为何忘掉一个人比坠入爱河难上千倍?
- 下一篇: 曾炜笔下那些引人入胜的小说作品
-
 标准误的计算方法是什么?资讯攻略11-08
标准误的计算方法是什么?资讯攻略11-08 -
 焊管重量计算的方法资讯攻略11-27
焊管重量计算的方法资讯攻略11-27 -
 余额宝的利息如何计算?资讯攻略11-13
余额宝的利息如何计算?资讯攻略11-13 -
 生死门公式是什么?求解!资讯攻略11-22
生死门公式是什么?求解!资讯攻略11-22 -
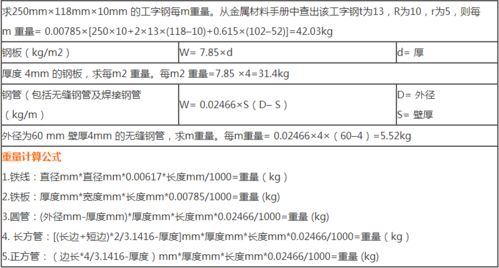 槽钢的重量是如何计算的?资讯攻略11-21
槽钢的重量是如何计算的?资讯攻略11-21 -
 微信余额宝收益如何计算资讯攻略11-14
微信余额宝收益如何计算资讯攻略11-14












